자료구조 5주차
Stack & Queue
Stack
- Insert/Delete만 제공
- Push/Pop이라고 부름
- Last in, First out
- 성능 : Push : O(1), Pop: O(1)
- Stack sort
- 가장 큰 값이 중앙, 가장 작은 값이 마지막에 있으면 수행 불가
stack<int> stackSort(stack<int> stk) {
stack<int> tempStk;
while(!stk.empty()) {
// 스택에서 하나씩 pop
int temp = stk.top();
stk.pop();
// tempStk이 비어있거나, tempStk의 top() 값이 temp보다 클 때까지 pop하여 tempStk에 push
while(!tempStk.empty() && tempStk.top() > temp) {
stk.push(tempStk.top());
tempStk.pop();
}
tempStk.push(temp);
}
return tempStk;
}Queue
- Insert/Delete만 제공
- First in, First out
- 성능 : Insert : O(1), Delete : O(1)
Stack 구현
- CPU 안에도 Stack이 존재 ( 함수 실행 과정에서 사용 )
#include <iostream>
int Stack[100];
int SP; // Stack Pointer
int init() { SP = 0; return 0; }
int isEmpty() { return SP == 0; }
int Push(int x) {
Stack[SP] = x;
SP++;
return 0;
}
int Pop() {
return Stack[--SP];
}Queue 구현
- Tail : 다음에 넣을 자리를 가리킴
- Head : 다음에 꺼낼 걸 가리킴
- h`ead, tail 앞 뒤가 바뀔 수도 있음
- head == tail 이면 꽉 찬 것 or 비어있는 것 , 구분 X
int Queue[100]; // N을 100으로
int Head, Tail;
int init() { Head = Tail = 0; return 0; }
int isEmpty() { return Head == Tail; }
int insertQueue(int x) {
Queue[Tail] = x;
Tail = (Tail + 1) % 100;
return 0;
}
int deleteQueue() {
int RetVal;
RetVal = Queue[Head];
Head = (Head + 1) % 100;
return RetVal;
}Stack , Queue 응용
- 미로찾기
- 대각선으로 가는 게 가능하다고 하자
- 전진이 정 안되면 후진
DFS 명시적 Stack 정확성
- (0,0)에서 어떤 위치 (s,t)로 가는 길이 있다.
- ↔ (0,0), (a1,b1), (a2,b2)…(s,t)인 좌표 sequence(연속)가 있고
- 인접한 쌍에서는 두 좌표가 각각 최대 1차이
- Map의 모든 좌표에 초기에 0이 적혀 있다.
- 위와 같은 상황에서 알고리즘은 (s,t)를 반드시 방문한다! 를 증명할 거
- “아니라고 가정”

DFS 명시적 Stack 성능
- 알고리즘이 진행되는 순서대로 생각하지 말고
- 한 칸에서 일어나는 일들을 따로 생각해보자
- 그 일들을 모든 칸에서 더하면 전체 시간이다.
BFS 명시적 Queue
- 갈림길이 나오면 양쪽으로 다 감
- 두 개의 할 일을 Queue에 넣어놈
과제 1 → DFS 명시적 Stack 사용해 미로찾기
#include <iostream>
using namespace std;
int Stack[10000];
int SP;
int init() { SP = 0; return 0; }
int isEmpty() { return SP == 0; }
void Push(int x) {
Stack[SP] = x;
SP++;
}
int Pop() {
return Stack[--SP];
}
char Map[101][101];
int M, N;
int Find(char Map[101][101]) {
int i, j;
int ip, jp;
i = j = 1; Map[i][j] = '*';
while (1) {
if (i == M && j == N)return 1;
ip = -100, jp = -100;
if (Map[i - 1][j-1] == '0') {
ip = i - 1; jp = j-1;
}
else if (Map[i - 1][j] == '0') {
ip = i - 1; jp = j;
}
else if (Map[i - 1][j + 1] == '0') {
ip = i - 1; jp = j + 1;
} // 위쪽 확인
else if (Map[i][j - 1] == '0') {
ip = i; jp = j - 1;
}
else if (Map[i][j + 1] == '0') {
ip = i; jp = j + 1;
} // 가운데 확인
else if (Map[i + 1][j - 1] == '0') {
ip = i + 1; jp = j - 1;
}
else if (Map[i + 1][j] == '0') {
ip = i + 1; jp = j;
}
else if (Map[i + 1][j + 1] == '0') {
ip = i + 1; jp = j + 1;
}// 밑에 확인
if (ip != -100) {
Push(i); Push(j);
i = ip; j = jp;
Map[i][j] = '*';
}
else {
if (isEmpty())
return -1;
Map[i][j] = 'X';
j = Pop(); i = Pop();
}
}
}
int main() {
// M,N은 100이하
cin >> M >> N;
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
char c;
cin >> c;
Map[i][j] = c;
}
}
Find(Map);
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
cout << Map[i][j] << " ";
}
cout << "\n";
}
}과제 2→BFS 명시적 Queue 이용해 미로찾기
#include <iostream>
using namespace std;
const int SIZE = 10000;
int Queue[SIZE];
int Head, Tail;
int init() { Head = Tail = 0; return 0; }
int isEmpty() { return Head == Tail; }
int insertQueue(int x) {
Queue[Tail] = x;
Tail = (Tail + 1) % SIZE;
return 0;
}
int deleteQueue() {
int RetVal;
RetVal = Queue[Head];
Head = (Head + 1) % SIZE;
return RetVal;
}
char Map[101][101];
int M, N;
int i, j;
void Find(char Map[101][101]) {
i = 1; j = 1;
while (1) {
if (Map[i][j] == '*') {
if (isEmpty()&&i==M&&j==N) {
cout<<"길을 찾았습니다!"<<"\n";
return;
}
else if(isEmpty()){
cout<<"길을 찾지 못했습니다!"<<"\n";
return;
}
else {
i = deleteQueue();
j = deleteQueue();
continue;
}
}
Map[i][j] = '*';
if (Map[i - 1][j - 1] == '0') {
insertQueue(i - 1);
insertQueue(j-1);
}
if (Map[i - 1][j] == '0') {
insertQueue(i - 1);
insertQueue(j);
}
if (Map[i - 1][j + 1] == '0') {
insertQueue(i - 1);
insertQueue(j+1);
} // 위쪽 확인
if (Map[i][j - 1] == '0') {
insertQueue(i);
insertQueue(j-1);
}
if (Map[i][j + 1] == '0') {
insertQueue(i);
insertQueue(j+1);
} // 가운데 확인
if (Map[i + 1][j - 1] == '0') {
insertQueue(i + 1);
insertQueue(j-1);
}
if (Map[i + 1][j] == '0') {
insertQueue(i + 1);
insertQueue(j);
}
if (Map[i + 1][j + 1] == '0') {
insertQueue(i + 1);
insertQueue(j+1);
}// 밑에 확인
if (isEmpty()) {
break;
}
i = deleteQueue();
j = deleteQueue();
}
}
int main() {
// M,N은 100이하
cin >> M >> N;
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
char c;
cin >> c;
Map[i][j] = c;
}
}
cout << "\n";
Find(Map);
cout << "\n";
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
cout << Map[i][j] << " ";
}
cout << "\n";
}
}2차시
Equivalence Relation
- Graph라는 자료구조를 다루고 있는 이야기
- Graph는 굉장히 많이 사용됨
- 똑같은 내용이더라도 … 약간 다른 관점에서 보는 것이 도움되는 경우 O
- 동치관계라는 제목으로 비유해서 시작해서 설명을 할 것
- 결국 → Stack, DFS를 가지고 응용을 해왔음. 똑같은 거를 다시하는 것
- But 약간 다른 Setting에서 진행
- 알고리즘이 다르면 성능차이가 여기선 발생 → 어떻게 다른 지?
Definition of Relation?
- 어떤 집합 A가 있을 때 , A*A의 부분집합을 뜻함 == Relation
- 순전히 집합으로만 정의된 관계를 생각할 수 있음
- Ex) A = {1,2,3,4}, R = {(1,3),(3,4),(1,1),(2,2)}
- A*A = {(1,1),(1,2)….(4,4)}
- R -) (1,3) == 1R3로 쓸 수 있음
An extreme example
- Relation < on N (Natural Numbers)
- < = { (1,2), (1,3), …, (2,3),(2,4)…}
- 2<4 means the same thing as (2,4) (- <
Equivalence Relation is when a Relation is…
- Reflexive : For all possible a, aRa ( 거울, 반사를 의미 )
- 모든 a에 대해서 aRa가 성립해야 됨.
- 어떤 특징이 같다.
- Symmetric(대칭) : For all possible a and b, aRb implies bRa
- aRb가 성립하면 brR도 성립!
- Transitive(전이) : For all possible a, b, and c, aRb, and bRc implies aRc
- 모든 a,b,c에 대해서 aRb가 성립하고 bRc가 성립하면 aRc도 성립!
직관적으로, Equivalence Relation은 어떤 특징들이 완전히 같은 관계로 생각될 수 있음 → People with same height, hair color, etc…
Induced(유도하다) Partition
- 우리가 풀려는 문제?
- Equivalence Relation을 입력으로 받아서, Partition을 찾으려는 것!
- 더 이상 늘릴 수 없는 부분집합들 ( 밑에는 성질 )
- aRb이면 a,b가 같은 부분집합에 있어야 되고,
- a,b가 같은 부분집합에 들어있으면 aRb가 성립되어야 함.
- 3개의 Partition 집합들이 존재
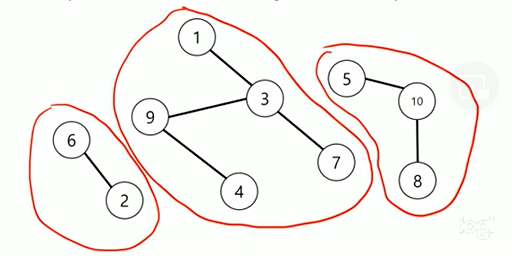
How to find Induced Partition?
- 입력은 동치관계가 성립하는 쌍들을 준다고 생각하자
- ( 따로 원소 개수는 주어짐 )
- ex ) 위 그림은 10(원소개수) 7(동치관계 성립 횟수) 을 처음에 입력받음
One Assumption
- Input is given in Minimal Form
- No deducible pairs are given ( 유추 가능한 쌍은 주어지지 않음 )
Let’s use DFS
- 결국 미로찾기랑 같음
- 시작은 아무데서나 할 수 있음
- 목적지는 없음 → 다 가보게 될 거
- 1번에서 시작했다고 하면 1번에서 줄이 그어져 있는 곳으로 갈 수 있음
- 코드 구현
#include <iostream>
#include <stack>
using namespace std;
int Arr[100][100];
int Mark[100]; // stack에 들어갔는 지 안 갔는지 확인
// int index[100];
int N, M; // N은 1부터 N까지 자료 개수, M은 Minimal Form
void Find(int a) {
int i;
Mark[a] = 1;
for (i = 1 ; i < N; i++) {
if (Arr[a][i] == 1&&Mark[i]==0) {
Find(i);
}
}
cout << a << ' ';
}
int main() {
cin >> N >> M;
int a, b;
for (int i = 0; i < M; i++) {
cin >> a >> b;
Arr[a][b] = 1;
Arr[b][a] = 1;
}
for (int i = 1; i <= N; i++) {
if (Mark[i] == 0) {
Find(i);
cout << '\n';
}
}
/*for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cout << Arr[i][j] << " ";
}
cout << "\n";
}*/
}- 이 알고리즘에서 입력형식이 꼭 Minimal Form일 필요는 없음
- 아니어도 잘 돌아감 ㅋㅋ
Performance Analysis
- Categorize time used ( Marker, Stack, Matrix 각각의 시간을 계산하고 더하자 )
- 노드 개수가 n개일 때 입력 size는 O(n)
- On the Marker
- Two options : DFS를 시작(O(n)번)할 때마다 … Start from beginning every time or remember last option
- Beginning : O(n^2)
- Remember : O(n) ← 지난 위치를 기억
- On the Stack
- O(n) ← (노드가 몇 번 들어갔다 나오는 지 생각 )
- == 각 node(item)은 1번씩 들어감
- On the Matrix
- Two options : Start from beginning every time or remember last location.
- At each Column : O(n^2) or O(n)(지난 위치 기억하면 )
- On the whole : O(n^2) either way
- == 각 열을 기준으로 보면 O(n)이 나올 수 있지만
- == 전체를 기준으로 보면 1의 개수가 최대 2*(n-2)이므로 (by Minimal 의 입력 사이즈 O(n) ) → O(n)개이다.
- == 맵 전체 시간 복잡도는 O(n^2*2)인데 O(n^2) 과 동일함
- 전체 시간 == O(n^2)
- ?? 너무 시간이 많이 걸리는데 =⇒ 0들을 버리고 1들만 가지고 있따면?
- how? → 누가 1인지 정보만을 가지고 있으면 된다. →using Vector코드 구현
#include <iostream>
#include <vector>
using namespace std;
int N, M;
vector<vector<int>> v;
vector<int> Mark;
void Find(int a) {
Mark[a] = 1;
int i;
for (i = 0; i < v[a].size(); i++) {
if (Mark[v[a][i]] == 0) {
Find(v[a][i]);
}
}
cout << a << " ";
}
int main() {
cin >> N >> M;
int a, b;
v.assign(N + 1, vector<int>()); // 빈 벡터
Mark.assign(N + 1, 0);
for (int i = 0; i < M; i++) {
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
}
for (int i = 1; i <= N; i++) {
if (Mark[i] == 0) {
Find(i);
cout << "\n";
}
}
/*for (int i = 0; i < N; i++) {
for (auto j = v[i].begin(); j < v[i].end(); j++) {
cout << *j << " ";
}
cout << "\n";
}*/
}- Categorize time used
- On the Marker
- Two options : DFS를 시작(O(n)번)할 때마다 … Start from beginning every time or remember last option
- Beginning : O(n^2)
- Remember : O(n) ← 지난 위치를 기억
- On the Stack
- O(n)
- On the Vector
- Two Options : Start from beginning every time or remember last location
- At each Row : O(n)
- On the whole : O(n^2) and O(n)
- Remember 한다면 vector의 총 원소는 최대 2n-2개가 되기 때문에 O(n)이 성립함
- On the Marker
- 전체 시간 == O(n^2) or O(n)
자료구조 5주차
Stack & Queue
Stack
- Insert/Delete만 제공
- Push/Pop이라고 부름
- Last in, First out
- 성능 : Push : O(1), Pop: O(1)
- Stack sort
- 가장 큰 값이 중앙, 가장 작은 값이 마지막에 있으면 수행 불가
stack<int> stackSort(stack<int> stk) {
stack<int> tempStk;
while(!stk.empty()) {
// 스택에서 하나씩 pop
int temp = stk.top();
stk.pop();
// tempStk이 비어있거나, tempStk의 top() 값이 temp보다 클 때까지 pop하여 tempStk에 push
while(!tempStk.empty() && tempStk.top() > temp) {
stk.push(tempStk.top());
tempStk.pop();
}
tempStk.push(temp);
}
return tempStk;
}Queue
- Insert/Delete만 제공
- First in, First out
- 성능 : Insert : O(1), Delete : O(1)
Stack 구현
- CPU 안에도 Stack이 존재 ( 함수 실행 과정에서 사용 )
#include <iostream>
int Stack[100];
int SP; // Stack Pointer
int init() { SP = 0; return 0; }
int isEmpty() { return SP == 0; }
int Push(int x) {
Stack[SP] = x;
SP++;
return 0;
}
int Pop() {
return Stack[--SP];
}Queue 구현
- Tail : 다음에 넣을 자리를 가리킴
- Head : 다음에 꺼낼 걸 가리킴
- h`ead, tail 앞 뒤가 바뀔 수도 있음
- head == tail 이면 꽉 찬 것 or 비어있는 것 , 구분 X
int Queue[100]; // N을 100으로
int Head, Tail;
int init() { Head = Tail = 0; return 0; }
int isEmpty() { return Head == Tail; }
int insertQueue(int x) {
Queue[Tail] = x;
Tail = (Tail + 1) % 100;
return 0;
}
int deleteQueue() {
int RetVal;
RetVal = Queue[Head];
Head = (Head + 1) % 100;
return RetVal;
}Stack , Queue 응용
- 미로찾기
- 대각선으로 가는 게 가능하다고 하자
- 전진이 정 안되면 후진
DFS 명시적 Stack 정확성
- (0,0)에서 어떤 위치 (s,t)로 가는 길이 있다.
- ↔ (0,0), (a1,b1), (a2,b2)…(s,t)인 좌표 sequence(연속)가 있고
- 인접한 쌍에서는 두 좌표가 각각 최대 1차이
- Map의 모든 좌표에 초기에 0이 적혀 있다.
- 위와 같은 상황에서 알고리즘은 (s,t)를 반드시 방문한다! 를 증명할 거
- “아니라고 가정”

DFS 명시적 Stack 성능
- 알고리즘이 진행되는 순서대로 생각하지 말고
- 한 칸에서 일어나는 일들을 따로 생각해보자
- 그 일들을 모든 칸에서 더하면 전체 시간이다.
BFS 명시적 Queue
- 갈림길이 나오면 양쪽으로 다 감
- 두 개의 할 일을 Queue에 넣어놈
과제 1 → DFS 명시적 Stack 사용해 미로찾기
#include <iostream>
using namespace std;
int Stack[10000];
int SP;
int init() { SP = 0; return 0; }
int isEmpty() { return SP == 0; }
void Push(int x) {
Stack[SP] = x;
SP++;
}
int Pop() {
return Stack[--SP];
}
char Map[101][101];
int M, N;
int Find(char Map[101][101]) {
int i, j;
int ip, jp;
i = j = 1; Map[i][j] = '*';
while (1) {
if (i == M && j == N)return 1;
ip = -100, jp = -100;
if (Map[i - 1][j-1] == '0') {
ip = i - 1; jp = j-1;
}
else if (Map[i - 1][j] == '0') {
ip = i - 1; jp = j;
}
else if (Map[i - 1][j + 1] == '0') {
ip = i - 1; jp = j + 1;
} // 위쪽 확인
else if (Map[i][j - 1] == '0') {
ip = i; jp = j - 1;
}
else if (Map[i][j + 1] == '0') {
ip = i; jp = j + 1;
} // 가운데 확인
else if (Map[i + 1][j - 1] == '0') {
ip = i + 1; jp = j - 1;
}
else if (Map[i + 1][j] == '0') {
ip = i + 1; jp = j;
}
else if (Map[i + 1][j + 1] == '0') {
ip = i + 1; jp = j + 1;
}// 밑에 확인
if (ip != -100) {
Push(i); Push(j);
i = ip; j = jp;
Map[i][j] = '*';
}
else {
if (isEmpty())
return -1;
Map[i][j] = 'X';
j = Pop(); i = Pop();
}
}
}
int main() {
// M,N은 100이하
cin >> M >> N;
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
char c;
cin >> c;
Map[i][j] = c;
}
}
Find(Map);
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
cout << Map[i][j] << " ";
}
cout << "\n";
}
}과제 2→BFS 명시적 Queue 이용해 미로찾기
#include <iostream>
using namespace std;
const int SIZE = 10000;
int Queue[SIZE];
int Head, Tail;
int init() { Head = Tail = 0; return 0; }
int isEmpty() { return Head == Tail; }
int insertQueue(int x) {
Queue[Tail] = x;
Tail = (Tail + 1) % SIZE;
return 0;
}
int deleteQueue() {
int RetVal;
RetVal = Queue[Head];
Head = (Head + 1) % SIZE;
return RetVal;
}
char Map[101][101];
int M, N;
int i, j;
void Find(char Map[101][101]) {
i = 1; j = 1;
while (1) {
if (Map[i][j] == '*') {
if (isEmpty()&&i==M&&j==N) {
cout<<"길을 찾았습니다!"<<"\n";
return;
}
else if(isEmpty()){
cout<<"길을 찾지 못했습니다!"<<"\n";
return;
}
else {
i = deleteQueue();
j = deleteQueue();
continue;
}
}
Map[i][j] = '*';
if (Map[i - 1][j - 1] == '0') {
insertQueue(i - 1);
insertQueue(j-1);
}
if (Map[i - 1][j] == '0') {
insertQueue(i - 1);
insertQueue(j);
}
if (Map[i - 1][j + 1] == '0') {
insertQueue(i - 1);
insertQueue(j+1);
} // 위쪽 확인
if (Map[i][j - 1] == '0') {
insertQueue(i);
insertQueue(j-1);
}
if (Map[i][j + 1] == '0') {
insertQueue(i);
insertQueue(j+1);
} // 가운데 확인
if (Map[i + 1][j - 1] == '0') {
insertQueue(i + 1);
insertQueue(j-1);
}
if (Map[i + 1][j] == '0') {
insertQueue(i + 1);
insertQueue(j);
}
if (Map[i + 1][j + 1] == '0') {
insertQueue(i + 1);
insertQueue(j+1);
}// 밑에 확인
if (isEmpty()) {
break;
}
i = deleteQueue();
j = deleteQueue();
}
}
int main() {
// M,N은 100이하
cin >> M >> N;
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
char c;
cin >> c;
Map[i][j] = c;
}
}
cout << "\n";
Find(Map);
cout << "\n";
for (int i = 1; i <= M; i++) {
for (int j = 1; j <= N; j++) {
cout << Map[i][j] << " ";
}
cout << "\n";
}
}2차시
Equivalence Relation
- Graph라는 자료구조를 다루고 있는 이야기
- Graph는 굉장히 많이 사용됨
- 똑같은 내용이더라도 … 약간 다른 관점에서 보는 것이 도움되는 경우 O
- 동치관계라는 제목으로 비유해서 시작해서 설명을 할 것
- 결국 → Stack, DFS를 가지고 응용을 해왔음. 똑같은 거를 다시하는 것
- But 약간 다른 Setting에서 진행
- 알고리즘이 다르면 성능차이가 여기선 발생 → 어떻게 다른 지?
Definition of Relation?
- 어떤 집합 A가 있을 때 , A*A의 부분집합을 뜻함 == Relation
- 순전히 집합으로만 정의된 관계를 생각할 수 있음
- Ex) A = {1,2,3,4}, R = {(1,3),(3,4),(1,1),(2,2)}
- A*A = {(1,1),(1,2)….(4,4)}
- R -) (1,3) == 1R3로 쓸 수 있음
An extreme example
- Relation < on N (Natural Numbers)
- < = { (1,2), (1,3), …, (2,3),(2,4)…}
- 2<4 means the same thing as (2,4) (- <
Equivalence Relation is when a Relation is…
- Reflexive : For all possible a, aRa ( 거울, 반사를 의미 )
- 모든 a에 대해서 aRa가 성립해야 됨.
- 어떤 특징이 같다.
- Symmetric(대칭) : For all possible a and b, aRb implies bRa
- aRb가 성립하면 brR도 성립!
- Transitive(전이) : For all possible a, b, and c, aRb, and bRc implies aRc
- 모든 a,b,c에 대해서 aRb가 성립하고 bRc가 성립하면 aRc도 성립!
직관적으로, Equivalence Relation은 어떤 특징들이 완전히 같은 관계로 생각될 수 있음 → People with same height, hair color, etc…
Induced(유도하다) Partition
- 우리가 풀려는 문제?
- Equivalence Relation을 입력으로 받아서, Partition을 찾으려는 것!
- 더 이상 늘릴 수 없는 부분집합들 ( 밑에는 성질 )
- aRb이면 a,b가 같은 부분집합에 있어야 되고,
- a,b가 같은 부분집합에 들어있으면 aRb가 성립되어야 함.
- 3개의 Partition 집합들이 존재

How to find Induced Partition?
- 입력은 동치관계가 성립하는 쌍들을 준다고 생각하자
- ( 따로 원소 개수는 주어짐 )
- ex ) 위 그림은 10(원소개수) 7(동치관계 성립 횟수) 을 처음에 입력받음
One Assumption
- Input is given in Minimal Form
- No deducible pairs are given ( 유추 가능한 쌍은 주어지지 않음 )
Let’s use DFS
- 결국 미로찾기랑 같음
- 시작은 아무데서나 할 수 있음
- 목적지는 없음 → 다 가보게 될 거
- 1번에서 시작했다고 하면 1번에서 줄이 그어져 있는 곳으로 갈 수 있음
- 코드 구현
#include <iostream>
#include <stack>
using namespace std;
int Arr[100][100];
int Mark[100]; // stack에 들어갔는 지 안 갔는지 확인
// int index[100];
int N, M; // N은 1부터 N까지 자료 개수, M은 Minimal Form
void Find(int a) {
int i;
Mark[a] = 1;
for (i = 1 ; i < N; i++) {
if (Arr[a][i] == 1&&Mark[i]==0) {
Find(i);
}
}
cout << a << ' ';
}
int main() {
cin >> N >> M;
int a, b;
for (int i = 0; i < M; i++) {
cin >> a >> b;
Arr[a][b] = 1;
Arr[b][a] = 1;
}
for (int i = 1; i <= N; i++) {
if (Mark[i] == 0) {
Find(i);
cout << '\n';
}
}
/*for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cout << Arr[i][j] << " ";
}
cout << "\n";
}*/
}- 이 알고리즘에서 입력형식이 꼭 Minimal Form일 필요는 없음
- 아니어도 잘 돌아감 ㅋㅋ
Performance Analysis
- Categorize time used ( Marker, Stack, Matrix 각각의 시간을 계산하고 더하자 )
- 노드 개수가 n개일 때 입력 size는 O(n)
- On the Marker
- Two options : DFS를 시작(O(n)번)할 때마다 … Start from beginning every time or remember last option
- Beginning : O(n^2)
- Remember : O(n) ← 지난 위치를 기억
- On the Stack
- O(n) ← (노드가 몇 번 들어갔다 나오는 지 생각 )
- == 각 node(item)은 1번씩 들어감
- On the Matrix
- Two options : Start from beginning every time or remember last location.
- At each Column : O(n^2) or O(n)(지난 위치 기억하면 )
- On the whole : O(n^2) either way
- == 각 열을 기준으로 보면 O(n)이 나올 수 있지만
- == 전체를 기준으로 보면 1의 개수가 최대 2*(n-2)이므로 (by Minimal 의 입력 사이즈 O(n) ) → O(n)개이다.
- == 맵 전체 시간 복잡도는 O(n^2*2)인데 O(n^2) 과 동일함
- 전체 시간 == O(n^2)
- ?? 너무 시간이 많이 걸리는데 =⇒ 0들을 버리고 1들만 가지고 있따면?
- how? → 누가 1인지 정보만을 가지고 있으면 된다. →using Vector코드 구현
#include <iostream>
#include <vector>
using namespace std;
int N, M;
vector<vector<int>> v;
vector<int> Mark;
void Find(int a) {
Mark[a] = 1;
int i;
for (i = 0; i < v[a].size(); i++) {
if (Mark[v[a][i]] == 0) {
Find(v[a][i]);
}
}
cout << a << " ";
}
int main() {
cin >> N >> M;
int a, b;
v.assign(N + 1, vector<int>()); // 빈 벡터
Mark.assign(N + 1, 0);
for (int i = 0; i < M; i++) {
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
}
for (int i = 1; i <= N; i++) {
if (Mark[i] == 0) {
Find(i);
cout << "\n";
}
}
/*for (int i = 0; i < N; i++) {
for (auto j = v[i].begin(); j < v[i].end(); j++) {
cout << *j << " ";
}
cout << "\n";
}*/
}- Categorize time used
- On the Marker
- Two options : DFS를 시작(O(n)번)할 때마다 … Start from beginning every time or remember last option
- Beginning : O(n^2)
- Remember : O(n) ← 지난 위치를 기억
- On the Stack
- O(n)
- On the Vector
- Two Options : Start from beginning every time or remember last location
- At each Row : O(n)
- On the whole : O(n^2) and O(n)
- Remember 한다면 vector의 총 원소는 최대 2n-2개가 되기 때문에 O(n)이 성립함
- On the Marker
- 전체 시간 == O(n^2) or O(n)
