1주차
[아래 강의를 참고한 내용을 바탕으로 기술하는 글입니다]
https://www.inflearn.com/course/10주완성-코딩테스트-큰돌/dashboard
재귀함수(About Recursion)
- 3가지 특징을 가진다.
- 정의 단계에서 자신을 재참조하는 함수
- 전달되는 상태인 매개변수가 달라질 뿐 똑같은 일을 하는 함수
- 큰 문제를 작은 부분문제로 나눠서 풀 때
- 피보나치 수열을 예시로 보자
#include <iostream>
#include <algorithm>
using namespace std;
int N;
int fibo(int n) {
if (n == 1 || n == 0) {
return n;
}
return fibo(n-1) + fibo(n-2);
}
int main() {
cin >> N;
cout << fibo(N) << "\n";
return 0;
}- 주의사항
- 반드시 기저사례를 써야 한다. (되도록 맨 앞에서 사용)
- 효율성 - 빠른 판단 후 종료
- 무한 재귀 방지
- 논리적 흐름
- 사이클이 있다면 쓰면 안된다.
- 반복문이 될 거 같으면 반복문으로 사용
- 반드시 기저사례를 써야 한다. (되도록 맨 앞에서 사용)

순열
- 순열이란?
- 서로 다른 n개의 원소에서 r(단, 0 < r ≤ n 0 < r \le n 0<r≤n일 때)개를 중복없이 순서를 고려하여 선택하거나 나열하거나 하는 것을 **순열**(permutation)이라고 한다.
[출처: https://namu.wiki/w/순열]
- 순열을 코드로 짜기 위해선 2가지 방법이 존재한다.
- next_permutation 함수 사용
- 재귀함수 사용
하나씩 살펴보자.
1. next_permutation
https://en.cppreference.com/w/cpp/algorithm/next_permutation
→ 새로운 순열이 이전 순열보다 사전순으로 큰 경우가 있을 때 까지 true를 반환하고 없다면 false를 반환한다고 생각하자.
→ 세번 째 파라미터 comp의 경우 custom으로 설정할 수 있다. default로 ‘operator <’를 사용해 순열을 생성하므로, 오름차순 순열을 생성한다.
→ 시간 복잡도의 경우 N/2 이다.
- 해당 함수 사용의 주의점
- 반드시 배열, 벡터를 정렬하고 사용해야 함.
- [first, last) 범위이므로 간단히 vector의 경우를 보면 [v.begin(), v.end())라고 생각할 수 있다.
- 코드
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
vector<int> v;
for(int i=0;i<3;i++) {
int a;
cin >> a;
v.push_back(a);
}
sort(v.begin(), v.end());
do {
for(int i : v) cout << i << " ";
cout << "\n";
}while(next_permutation(v.begin(), v.end()));
return 0;
}재귀를 이용한 순열
- 우선 코드를 보자
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> v;
void printV() {
for(int i:v) cout << i << " ";
cout << "\n";
return ;
}
void makePermutation(int n, int r, int depth) {
if (r == depth) {
printV();
}
// 각 depth에 대해 남아 있는 것들 중에 모두 뽑아보고,
// 해당 경우에 대해 재귀적으로 makePermutation 함수를 돌리고,
// 원상복구 하여 다시 경우의 수를 찾는다
for(int i = depth; i < n; i++) {
swap(v[i], v[depth]);
makePermutation(n, r, depth + 1);
swap(v[i], v[depth]);
}
return ;
}
int main() {
for(int i=0;i<3;i++) {
int a;
cin >> a;
v.push_back(a);
}
sort(v.begin(), v.end());
makePermutation(3, 3, 0);
return 0;
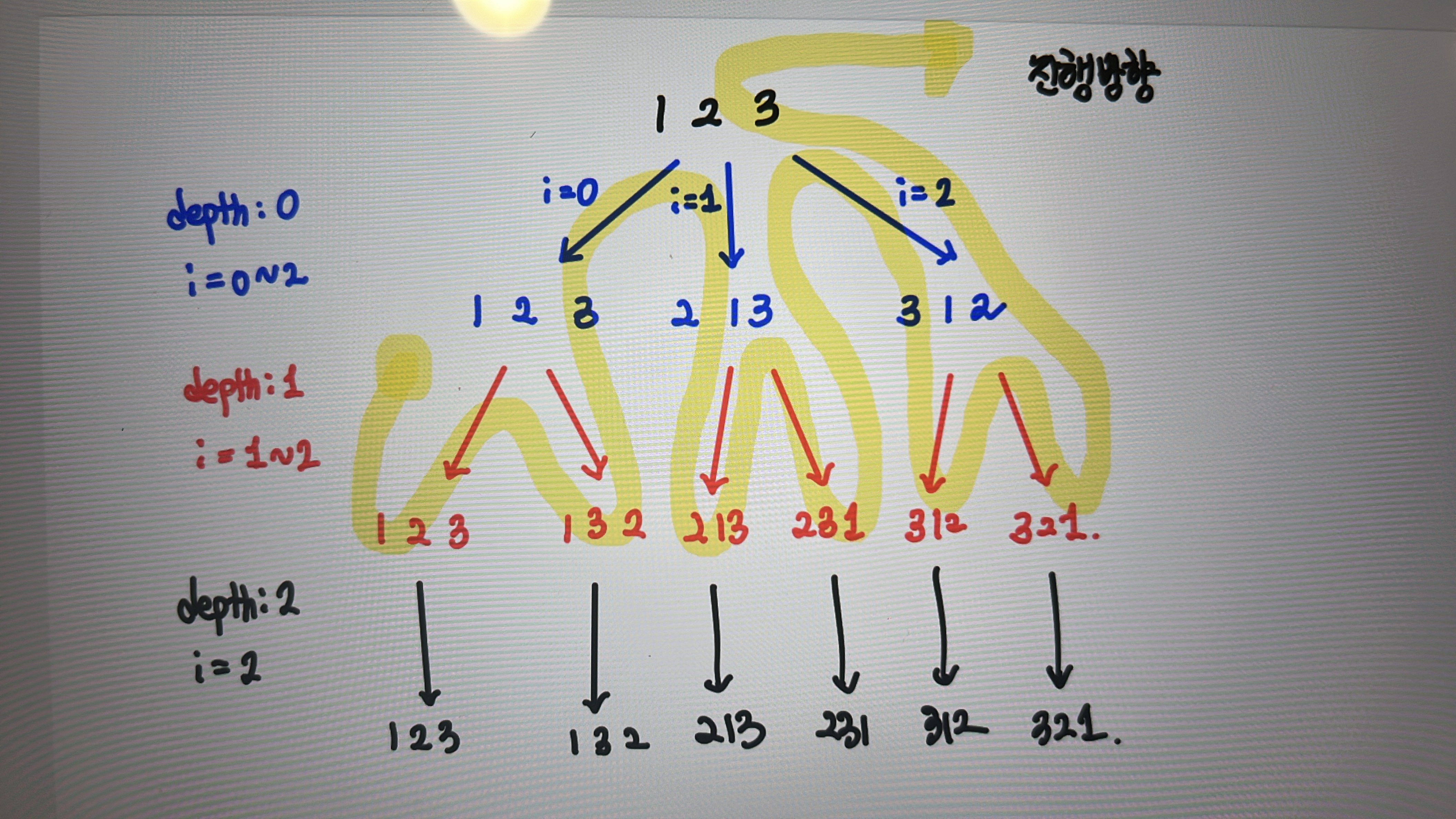
}- 코드의 흐름은 아래 그림과 같다.
조합
- 조합이란?
- n개의 원소를 갖는 집합에서 r개의 원소를 선택하는 것 혹은 선택의 결과로 정의
[출처: https://namu.wiki/w/조합]
- 조합을 코드로 작성하는 방법은 대표적으로 2가지가 존재
- 재귀를 이용한 조합
- 반복문을 이용한 조합 (3개 이하를 고를 땐 이걸 쓰자)
[재귀를 이용한 조합]
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int n = 5, k = 3, a[5] = {1, 2, 3, 4, 5};
vector<int> b;
void printV() {
for(int i:b) cout<< i << " ";
cout << "\n";
return ;
}
void combi(int start) {
if (b.size() == k) {
printV();
return;
}
for(int i = start + 1; i < n; i++) {
b.push_back(i);
combi(i);
b.pop_back();
}
return ;
}
int main() {
combi(-1);
return 0;
}- 파라미터로 존재하는 start는 vector b의 인덱스를 뜻한다.
[반복문을 이용한 조합]
- 중첩 for문을 사용한다.
- 그래서 적당히 원소가 작다면 편하게 쓸 수 있다.
#include <bits/stdc++.h>
using namespace std;
int n = 5;
int k = 3;
int a[5] = {1, 2, 3, 4, 5};
int main() {
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j++){
for(int k = j + 1; k < n; k++){
cout << i << " " << j << " " << k << '\n';
}
}
}
return 0;
}unique
- 범위안의 있는 요소 중에서 앞에서부터 서로를 비교해가며 중복되는 요소를 제거하고, 나머지 요소들은 삭제하지 않고 그대로 두는 함수
- O(n)의 시간복잡도를 가짐
- 간단하게 사용 코드로만 보자.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
vector<int> v {4, 3, 3, 5, 1, 2, 3};
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for(int i: v) cout << i << " ";
cout << "\n";
return 0;
}
// 1 2 3 4 5참고
- array to pointer decay
- 배열이 포인터로 부식되는 현상으로…
- 배열의 이름을 포인터에 할당하게 되면 배열 크기 정보는 날라가고 첫 번째 요소의 주소만 해당 포인터에 바인딩되는 현상이다.
- +1, +2 … 등을 하게 된다면 주소를 이동하면서 사용할 수도 있다.
'PS' 카테고리의 다른 글
| [스터디] - 4회차 (1) | 2024.04.05 |
|---|---|
| [스터디 - 3회차] (0) | 2024.03.29 |
| [스터디] - 2회차 (0) | 2024.03.20 |
1주차
[아래 강의를 참고한 내용을 바탕으로 기술하는 글입니다]
https://www.inflearn.com/course/10주완성-코딩테스트-큰돌/dashboard
재귀함수(About Recursion)
- 3가지 특징을 가진다.
- 정의 단계에서 자신을 재참조하는 함수
- 전달되는 상태인 매개변수가 달라질 뿐 똑같은 일을 하는 함수
- 큰 문제를 작은 부분문제로 나눠서 풀 때
- 피보나치 수열을 예시로 보자
#include <iostream>
#include <algorithm>
using namespace std;
int N;
int fibo(int n) {
if (n == 1 || n == 0) {
return n;
}
return fibo(n-1) + fibo(n-2);
}
int main() {
cin >> N;
cout << fibo(N) << "\n";
return 0;
}- 주의사항
- 반드시 기저사례를 써야 한다. (되도록 맨 앞에서 사용)
- 효율성 - 빠른 판단 후 종료
- 무한 재귀 방지
- 논리적 흐름
- 사이클이 있다면 쓰면 안된다.
- 반복문이 될 거 같으면 반복문으로 사용
- 반드시 기저사례를 써야 한다. (되도록 맨 앞에서 사용)

순열
- 순열이란?
- 서로 다른 n개의 원소에서 r(단, 0 < r ≤ n 0 < r \le n 0<r≤n일 때)개를 중복없이 순서를 고려하여 선택하거나 나열하거나 하는 것을 **순열**(permutation)이라고 한다.
[출처: https://namu.wiki/w/순열]
- 순열을 코드로 짜기 위해선 2가지 방법이 존재한다.
- next_permutation 함수 사용
- 재귀함수 사용
하나씩 살펴보자.
1. next_permutation
https://en.cppreference.com/w/cpp/algorithm/next_permutation
→ 새로운 순열이 이전 순열보다 사전순으로 큰 경우가 있을 때 까지 true를 반환하고 없다면 false를 반환한다고 생각하자.
→ 세번 째 파라미터 comp의 경우 custom으로 설정할 수 있다. default로 ‘operator <’를 사용해 순열을 생성하므로, 오름차순 순열을 생성한다.
→ 시간 복잡도의 경우 N/2 이다.
- 해당 함수 사용의 주의점
- 반드시 배열, 벡터를 정렬하고 사용해야 함.
- [first, last) 범위이므로 간단히 vector의 경우를 보면 [v.begin(), v.end())라고 생각할 수 있다.
- 코드
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
vector<int> v;
for(int i=0;i<3;i++) {
int a;
cin >> a;
v.push_back(a);
}
sort(v.begin(), v.end());
do {
for(int i : v) cout << i << " ";
cout << "\n";
}while(next_permutation(v.begin(), v.end()));
return 0;
}재귀를 이용한 순열
- 우선 코드를 보자
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> v;
void printV() {
for(int i:v) cout << i << " ";
cout << "\n";
return ;
}
void makePermutation(int n, int r, int depth) {
if (r == depth) {
printV();
}
// 각 depth에 대해 남아 있는 것들 중에 모두 뽑아보고,
// 해당 경우에 대해 재귀적으로 makePermutation 함수를 돌리고,
// 원상복구 하여 다시 경우의 수를 찾는다
for(int i = depth; i < n; i++) {
swap(v[i], v[depth]);
makePermutation(n, r, depth + 1);
swap(v[i], v[depth]);
}
return ;
}
int main() {
for(int i=0;i<3;i++) {
int a;
cin >> a;
v.push_back(a);
}
sort(v.begin(), v.end());
makePermutation(3, 3, 0);
return 0;
}- 코드의 흐름은 아래 그림과 같다.

조합
- 조합이란?
- n개의 원소를 갖는 집합에서 r개의 원소를 선택하는 것 혹은 선택의 결과로 정의
[출처: https://namu.wiki/w/조합]
- 조합을 코드로 작성하는 방법은 대표적으로 2가지가 존재
- 재귀를 이용한 조합
- 반복문을 이용한 조합 (3개 이하를 고를 땐 이걸 쓰자)
[재귀를 이용한 조합]
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int n = 5, k = 3, a[5] = {1, 2, 3, 4, 5};
vector<int> b;
void printV() {
for(int i:b) cout<< i << " ";
cout << "\n";
return ;
}
void combi(int start) {
if (b.size() == k) {
printV();
return;
}
for(int i = start + 1; i < n; i++) {
b.push_back(i);
combi(i);
b.pop_back();
}
return ;
}
int main() {
combi(-1);
return 0;
}- 파라미터로 존재하는 start는 vector b의 인덱스를 뜻한다.
[반복문을 이용한 조합]
- 중첩 for문을 사용한다.
- 그래서 적당히 원소가 작다면 편하게 쓸 수 있다.
#include <bits/stdc++.h>
using namespace std;
int n = 5;
int k = 3;
int a[5] = {1, 2, 3, 4, 5};
int main() {
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j++){
for(int k = j + 1; k < n; k++){
cout << i << " " << j << " " << k << '\n';
}
}
}
return 0;
}unique
- 범위안의 있는 요소 중에서 앞에서부터 서로를 비교해가며 중복되는 요소를 제거하고, 나머지 요소들은 삭제하지 않고 그대로 두는 함수
- O(n)의 시간복잡도를 가짐
- 간단하게 사용 코드로만 보자.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
vector<int> v {4, 3, 3, 5, 1, 2, 3};
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for(int i: v) cout << i << " ";
cout << "\n";
return 0;
}
// 1 2 3 4 5참고
- array to pointer decay
- 배열이 포인터로 부식되는 현상으로…
- 배열의 이름을 포인터에 할당하게 되면 배열 크기 정보는 날라가고 첫 번째 요소의 주소만 해당 포인터에 바인딩되는 현상이다.
- +1, +2 … 등을 하게 된다면 주소를 이동하면서 사용할 수도 있다.
'PS' 카테고리의 다른 글
| [스터디] - 4회차 (1) | 2024.04.05 |
|---|---|
| [스터디 - 3회차] (0) | 2024.03.29 |
| [스터디] - 2회차 (0) | 2024.03.20 |
